Tideman

Problema a resolver

Você já sabe sobre eleições por pluralidade, que seguem um algoritmo muito simples para determinar o vencedor de uma eleição: cada eleitor tem um voto, e o candidato com mais votos vence.

Mas o voto de pluralidade tem algumas desvantagens. O que acontece, por exemplo, em uma eleição com três candidatos e as cédulas abaixo são lançadas?

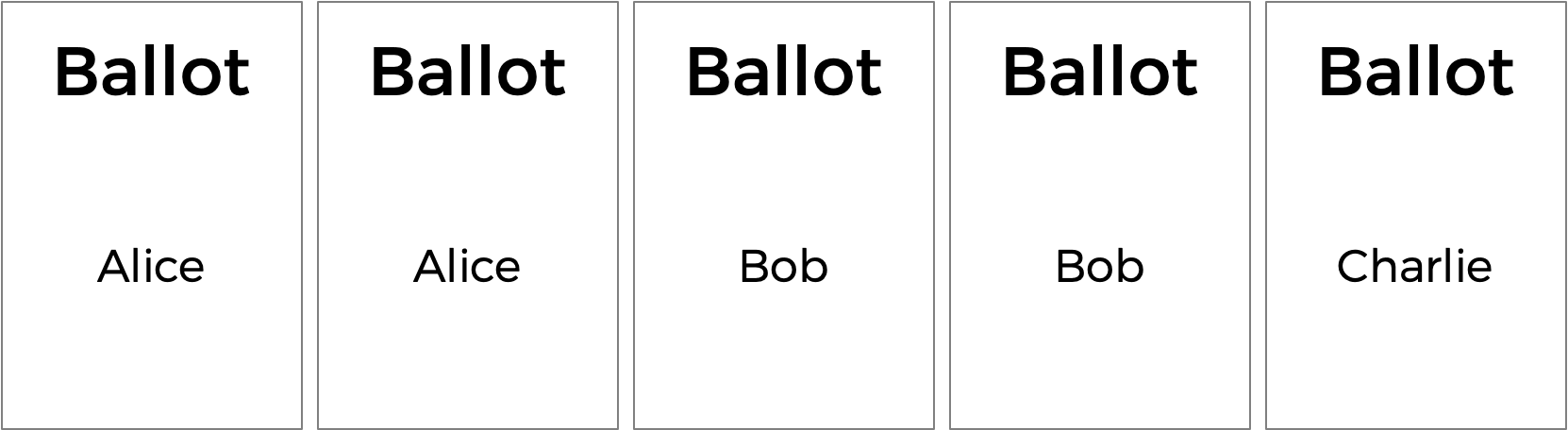
Uma votação por pluralidade declararia aqui um empate entre Alice e Bob, uma vez que cada um tem dois votos. Mas esse é o resultado certo?

Existe outro tipo de sistema de votação conhecido como sistema de votação por classificação. Em um sistema de classificação, os eleitores podem votar em mais de um candidato. Em vez de apenas votar em sua primeira escolha, eles podem classificar os candidatos em ordem de preferência. As cédulas resultantes podem, portanto, se parecer com as abaixo.

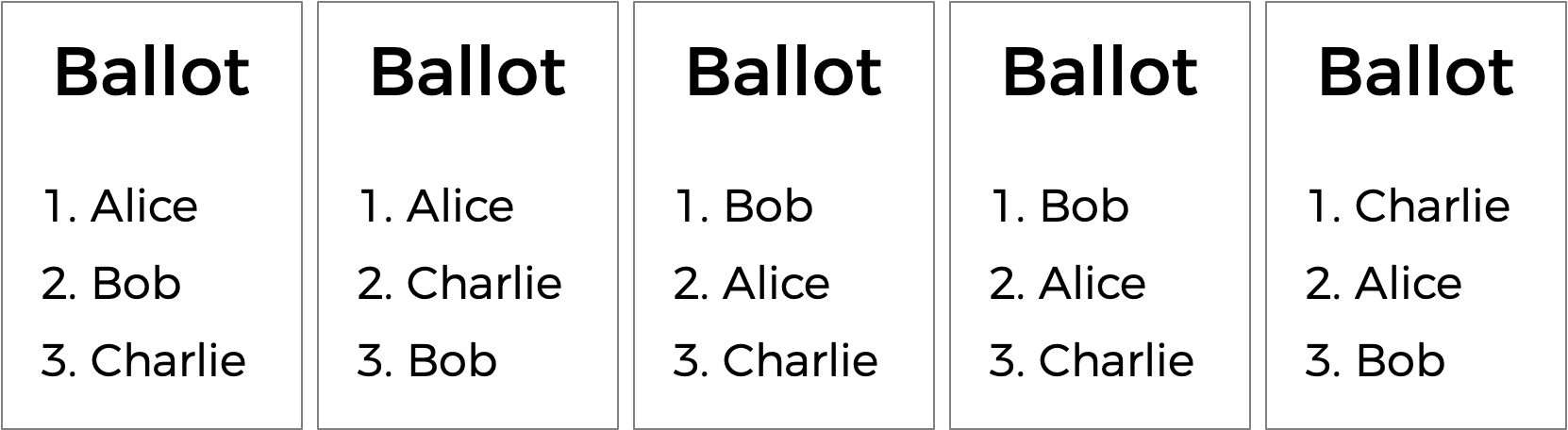
Aqui, cada eleitor, além de especificar seu candidato de primeira preferência, também indicou sua segunda e terceira escolhas. E agora, o que antes era uma eleição empatada pode agora ter um vencedor. A corrida foi originalmente empatada entre Alice e Bob. Mas o eleitor que escolheu Charlie preferiu Alice a Bob, então Alice poderia ser declarada a vencedora aqui.

A votação por classificação também pode resolver outra possível desvantagem da votação por pluralidade. Dê uma olhada nas cédulas a seguir.

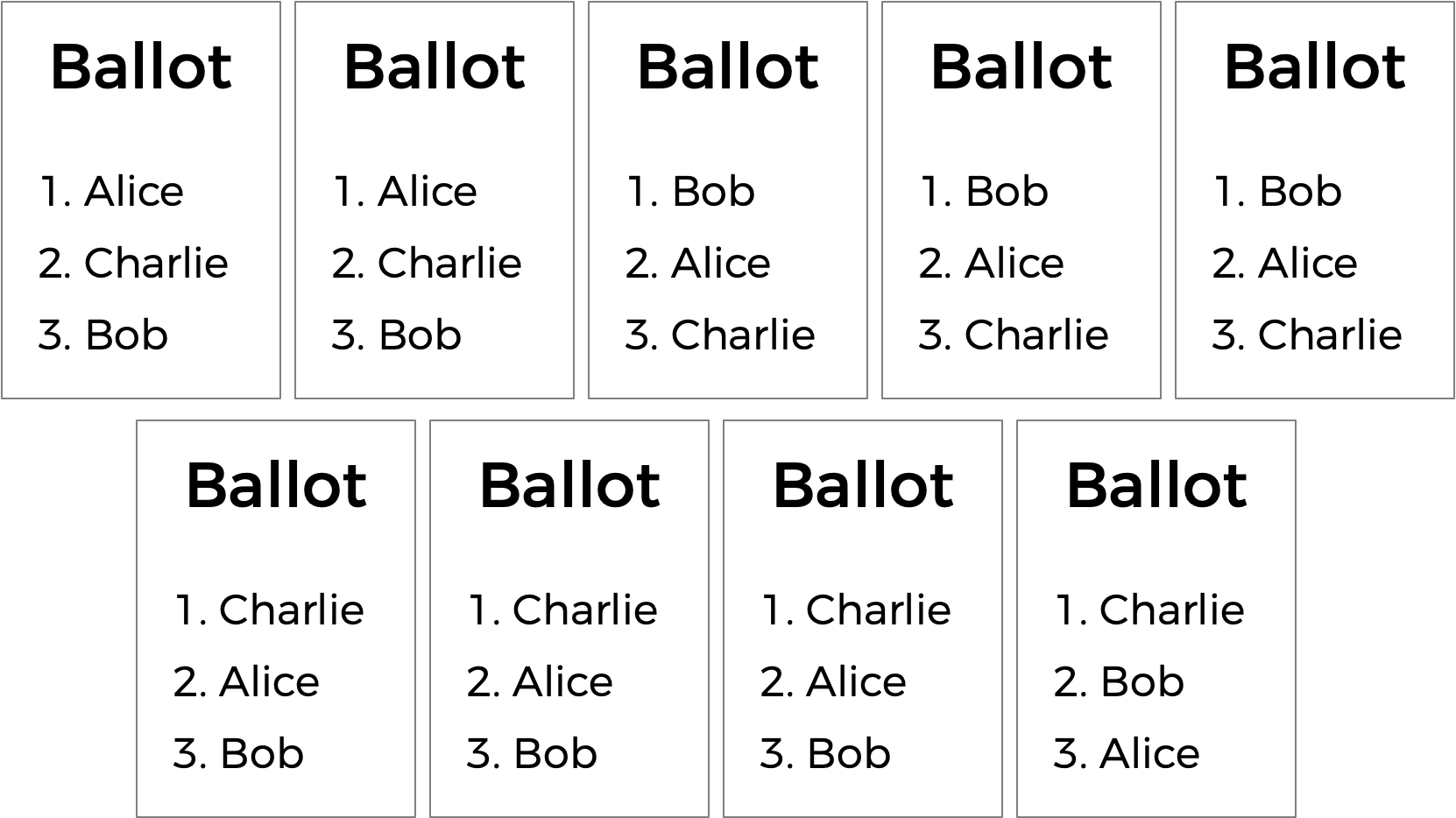
Quem deve ganhar esta eleição? Em uma votação por pluralidade, onde cada eleitor escolhe apenas sua primeira preferência, Charlie vence esta eleição com quatro votos, em comparação com apenas três para Bob e dois para Alice. (Observe que, se você estiver familiarizado com o sistema de votação por segundo turno instantâneo, Charlie também vence aqui sob esse sistema). Alice, no entanto, poderia razoavelmente argumentar que ela deveria ser a vencedora da eleição em vez de Charlie: afinal, dos nove eleitores, a maioria (cinco deles) preferia Alice a Charlie, então a maioria das pessoas ficaria mais feliz com Alice como vencedora em vez de Charlie.

Alice é, nesta eleição, a chamada "vencedora de Condorcet" da eleição: a pessoa que teria vencido qualquer confronto direto contra outro candidato. Se a eleição tivesse sido apenas Alice e Bob, ou apenas Alice e Charlie, Alice teria vencido.

O método de voto Tideman (também conhecido como "pares classificados") é um método de voto por classificação que garante produzir o vencedor de Condorcet da eleição, se houver um. Em um arquivo chamado tideman.c em uma pasta chamada tideman, crie um programa para simular uma eleição pelo método de votação Tideman.

Demonstração

Código de distribuição

Faça login em cs50.dev, clique na janela do seu terminal e executecd por conta própria. Você deve descobrir que o prompt da janela do seu terminal se parece com o seguinte:

  $

Execute em seguida

  wget https://cdn.cs50.net/2023/fall/psets/3/tideman.zip

para baixar um ZIP chamado tideman.zip em seu espaço de código.

Em seguida, execute

  unzip tideman.zip

para criar uma pasta chamada tideman. Você não precisa mais do arquivo ZIP, então você pode executar

  rm tideman.zip

e responda com "s" seguido de Enter no prompt para remover o arquivo ZIP que você baixou.

Agora digite

  cd tideman

seguido de Enter para se mover (ou seja, abrir) esse diretório. Seu prompt agora deve se parecer com o seguinte.

  tideman/ $

Se tudo foi bem-sucedido, você deve executar

  ls

e ver um arquivo chamado tideman.c. Executar code tideman.c deve abrir o arquivo onde você irá digitar seu código para este conjunto de problemas. Se não, refaça seus passos e veja se você pode determinar onde errou!

Contexto

De forma geral, o método Tideman funciona construindo um "gráfico" de candidatos, onde uma seta (ou seja, uma aresta) do candidato A para o candidato B indica que o candidato A vence o candidato B em um confronto direto. O gráfico para a eleição acima, então, se pareceria com o abaixo.

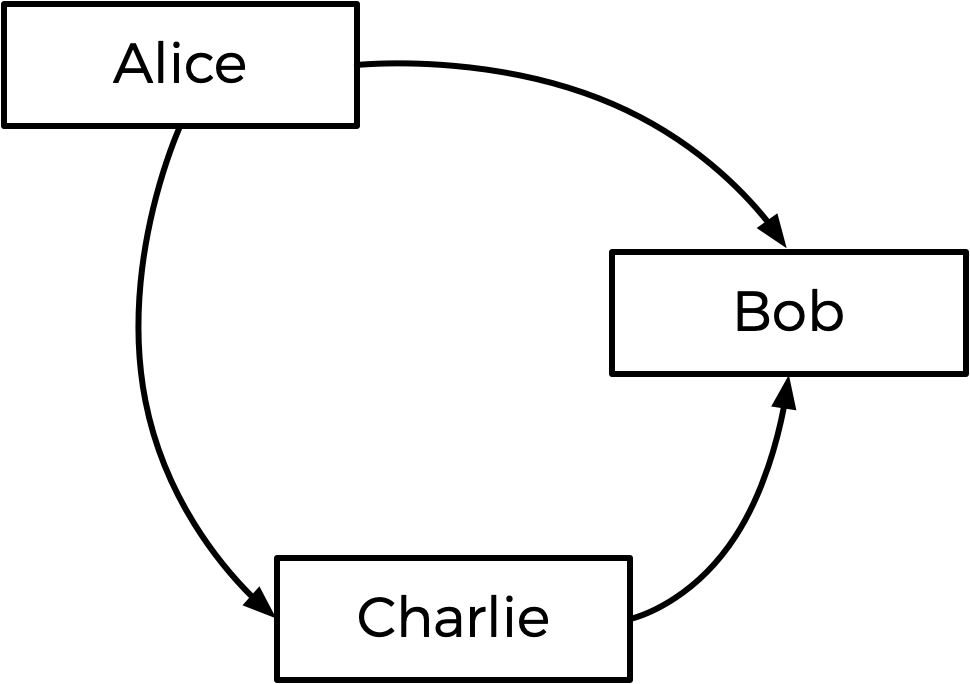
A seta de Alice para Bob significa que mais eleitores preferem Alice a Bob (5 preferem Alice, 4 preferem Bob). Da mesma forma, as outras setas significam que mais eleitores preferem Alice a Charlie, e mais eleitores preferem Charlie a Bob.

Olhando para este gráfico, o método Tideman afirma que o vencedor da eleição deve ser a "fonte" do gráfico (ou seja, o candidato que não tem nenhuma seta apontando para ele). Neste caso, a fonte é Alice — Alice é a única que não tem nenhuma seta apontando para ela, o que significa que ninguém é preferido em um confronto direto com Alice. Alice é, portanto, declarada a vencedora da eleição.

No entanto, é possível que, quando as setas forem desenhadas, não haja um vencedor de Condorcet. Considere as cédulas abaixo.

Entre Alice e Bob, Alice é preferida a Bob por uma margem de 7-2. Entre Bob e Charlie, Bob é preferido a Charlie por uma margem de 5-4. Mas entre Charlie e Alice, Charlie é preferido a Alice por uma margem de 6-3. Se desenharmos o gráfico, não há nenhuma fonte! Temos um ciclo de candidatos, onde Alice vence Bob, que vence Charlie, que vence Alice (bem parecido com um jogo de pedra-papel-tesoura). Neste caso, parece que não há como escolher um vencedor.

Para lidar com isso, o algoritmo Tideman deve ter cuidado para evitar a criação de ciclos no gráfico de candidatos. Como ele faz isso? O algoritmo bloqueia as arestas mais fortes primeiro, já que elas são indiscutivelmente as mais significativas. Em particular, o algoritmo Tideman especifica que as arestas de confronto devem ser "bloqueadas" no gráfico uma de cada vez, com base na "força" da vitória (quanto mais pessoas preferirem um candidato em relação ao seu oponente, mais forte será a vitória). Desde que a aresta possa ser bloqueada no gráfico sem criar um ciclo, a aresta é adicionada; caso contrário, a aresta é ignorada.

Como isso funcionaria no caso dos votos acima? Bem, a maior margem de vitória para um par é Alice vencendo Bob, já que 7 eleitores preferem Alice a Bob (nenhum outro confronto direto tem um vencedor preferido por mais de 7 eleitores). Então, a seta Alice-Bob é bloqueada no gráfico primeiro. A próxima maior margem de vitória é a vitória de 6-3 de Charlie sobre Alice, então essa seta é bloqueada em seguida.

O próximo passo é a vitória de 5-4 de Bob sobre Charlie. Mas observe: se adicionássemos uma seta de Bob para Charlie agora, criaríamos um ciclo! Como o gráfico não pode permitir ciclos, devemos pular esta aresta e não adicioná-la ao gráfico. Se houvesse mais setas a serem consideradas, olharíamos para elas em seguida, mas essa foi a última seta, então o gráfico está completo.

Este processo passo a passo é mostrado abaixo, com o gráfico final à direita.

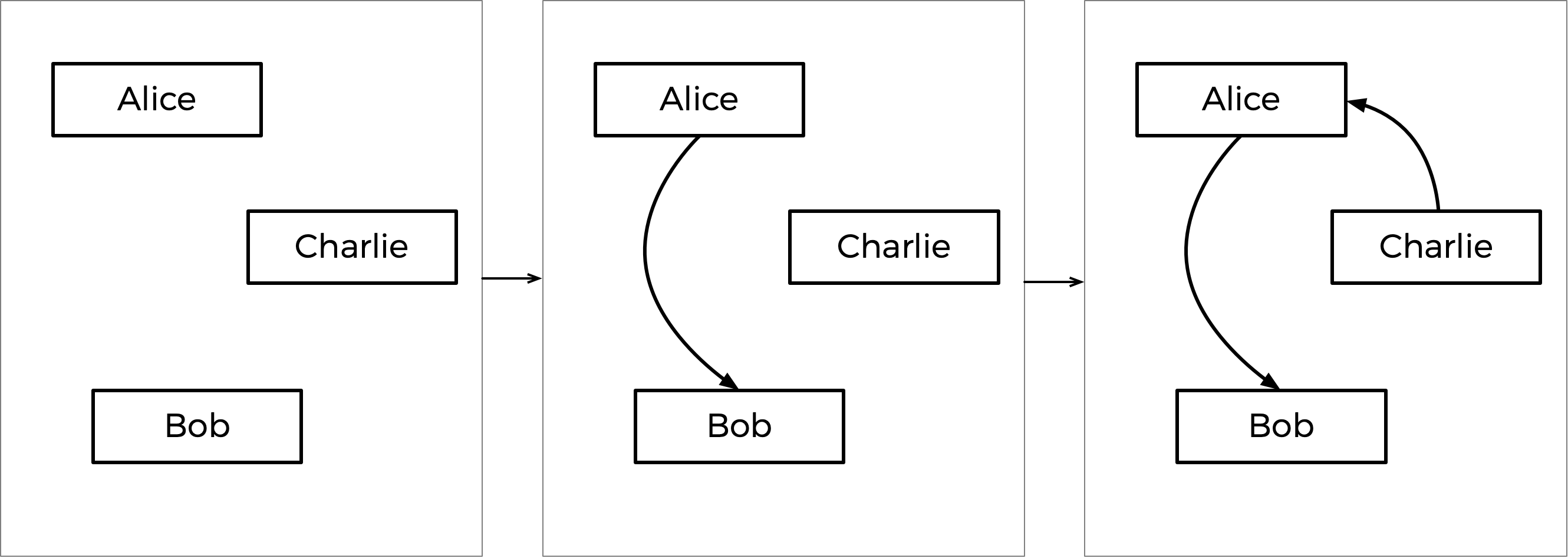
Com base no gráfico resultante, Charlie é a fonte (não há nenhuma seta apontando para Charlie), então Charlie é declarado o vencedor desta eleição.

De forma mais formal, o método de votação Tideman consiste em três partes:

• Contagem: Uma vez que todos os eleitores tenham indicado todas as suas preferências, determine, para cada par de candidatos, quem é o candidato preferido e por qual margem ele é preferido.
• Classificação: Classifique os pares de candidatos em ordem decrescente de força de vitória, onde a força de vitória é definida como o número de eleitores que preferem o candidato preferido.
• Bloqueio: Começando com o par mais forte, percorra os pares de candidatos em ordem e "bloqueie" cada par no gráfico de candidatos, desde que o bloqueio daquele par não crie um ciclo no gráfico.

Quando o gráfico estiver completo, a fonte do gráfico (aquele sem arestas apontando para ele) é o vencedor!

Compreensão

Vamos dar uma olhada no tideman.c.

Primeiro, observe o array bidimensional preferences. O inteiro preferences[i][j] representará o número de eleitores que preferem o candidato i ao candidato j.

O arquivo também define outro array bidimensional, chamado locked, que representará o gráfico de candidatos. locked é um array booleano, portanto locked[i][j] sendo true representa a existência de uma aresta apontando do candidato i para o candidato j; false significa que não há aresta. (Se curioso, esta representação de um gráfico é conhecida como “matriz de adjacência”).

Em seguida, vem um struct chamado pair, usado para representar um par de candidatos: cada par inclui o índice do candidato winner (vencedor) e o índice do candidato loser (perdedor).

Os próprios candidatos são armazenados no array candidates, que é um array de strings representando os nomes de cada um dos candidatos. Há também um array de pairs, que representará todos os pares de candidatos (para os quais um é preferido ao outro) na eleição.

O programa também tem duas variáveis globais: pair_count e candidate_count, representando o número de pares e o número de candidatos nos arrays pairs e candidates, respectivamente.

Agora no main. Observe que, após determinar o número de candidatos, o programa percorre o gráfico locked e inicialmente define todos os valores como false, o que significa que nosso gráfico inicial não terá arestas.

Em seguida, o programa percorre todos os eleitores e coleta suas preferências em um array chamado ranks (por meio de uma chamada para vote), onde ranks[i] é o índice do candidato que é a i-ésima preferência para o eleitor. Essas classificações são passadas para a função record_preference, cujo trabalho é pegar essas classificações e atualizar a variável global preferences.

Depois que todos os votos forem contabilizados, os pares de candidatos são adicionados ao array pairs por meio de uma chamada para add_pairs, classificados por meio de uma chamada para sort_pairs e bloqueados no gráfico por meio de uma chamada para lock_pairs. Finalmente, print_winner é chamado para imprimir o nome do vencedor da eleição!

Mais adiante no arquivo, você verá que as funções vote, record_preference, add_pairs,sort_pairs, lock_pairs e print_winner são deixadas em branco. Isso é com você!

Especificação

Conclua a implementação de tideman.c de forma que simule uma eleição Tideman.

• Conclua a função vote.
• A função usa os argumentos rank, name e ranks. Se name for uma correspondência com o nome de um candidato válido, você deve atualizar o array ranks para indicar que o eleitor tem o candidato como sua preferência rank (onde 0 é a primeira preferência, 1 é a segunda preferência, etc.)
• Lembre-se que ranks[i] aqui representa a i-ésima preferência do usuário.
• A função deve retornar true se a classificação foi registrada com sucesso e false caso contrário (se, por exemplo, name não for o nome de um dos candidatos).
• Você pode presumir que nenhum dois candidatos terão o mesmo nome.
• Conclua a função record_preferences.
• A função é chamada uma vez para cada eleitor e recebe como argumento o array ranks, (lembre-se que ranks[i] é a i-ésima preferência do eleitor, onde ranks[0] é a primeira preferência).
• A função deve atualizar o array global preferences para adicionar as preferências do eleitor atual. Lembre-se que preferences[i][j] deve representar o número de eleitores que preferem o candidato i ao candidato j.
• Você pode presumir que cada eleitor classificará cada um dos candidatos.
• Conclua a função add_pairs.
• A função deve adicionar todos os pares de candidatos em que um candidato é o preferido ao array pairs. Um par de candidatos que estão empatados (um não é preferido ao outro) não deve ser adicionado ao array.
• A função deve atualizar a variável global pair_count para que seja o número de pares de candidatos. (Os pares devem, portanto, todos ser armazenados entre pares[0] e pares[pair_count - 1], inclusive).
• Conclua a função sort_pairs.
• A função deve classificar o array pairs em ordem decrescente de força da vitória, onde a força da vitória é definida pelo número de eleitores que preferem o candidato preferido. Se vários pares tiverem a mesma força de vitória, você pode presumir que a ordem não importa.
• Conclua a função lock_pairs.
• A função deve criar o gráfico locked, adicionando todas as arestas em ordem decrescente de força da vitória desde que a aresta não crie um ciclo.
• Conclua a função print_winner.
• A função deve imprimir o nome do candidato que é a fonte do gráfico. Você pode presumir que não haverá mais de uma fonte.

Você não deve modificar nada mais em tideman.c além das implementações das funções vote, record_preferences, add_pairs, sort_pairs, lock_pairs e print_winner (e a inclusão de arquivos de cabeçalho adicionais, se quiser). Você tem permissão para adicionar funções adicionais ao tideman.c, desde que não altere as declarações de nenhuma das funções existentes.

Passo a passo

Como testar

Certifique-se de testar seu código para garantir que ele lida com…

• Uma eleição com qualquer número de candidatos (até o MAX de 9)
• Voto para um candidato pelo nome
• Votos inválidos para candidatos que não estão na cédula
• Imprimindo o vencedor da eleição

Correção

  check50 cs50/problemas/2024/x/tideman

Estilo

  style50 tideman.c

Como enviar

  submit50 cs50/problemas/2024/x/tideman