Aula 3

• Busca
• Grande O
• Busca linear
• Estruturas
• Ordenação
• Ordenação por seleção
• Recursão
• Ordenação por mesclagem

Busca

• Da última vez, falamos sobre a memória em um computador ou RAM e sobre como nossos dados podem ser armazenados como variáveis ​​individuais ou como matrizes de muitos itens ou elementos.
• Podemos pensar em uma matriz com vários itens como uma fileira de armários, onde um computador só pode abrir um armário para olhar um item, um de cada vez.
• Por exemplo, se quisermos verificar se um número está em uma matriz, com um algoritmo que utiliza uma matriz como entrada e produz um booleano como resultado, podemos:
  • examinar cada armário ou cada elemento, um de cada vez, do início ao fim.
    • Isso é chamado de busca linear, em que nos movemos em uma linha, já que nossa matriz não é classificada.
  • iniciar no meio e mover para a esquerda ou direita dependendo do que estamos procurando, se nossa matriz de itens for classificada.
    • Isso é chamado de busca binária, já que podemos dividir nosso problema em dois a cada passo, como Davi fez com a lista telefônica na semana 0.

• Podemos escrever pseudocódigo para a busca linear com:

    Para i de 0 a n – 1
        Se o i-ésimo elemento for 50
            Retornar verdadeiro
    Retornar falso
  

  • Podemos rotular cada um dos n armários de 0 a n – 1 e verificar cada um deles em ordem.

• Para a busca binária, nosso algoritmo pode ter a seguinte aparência:

    Se não houver itens
        Retornar falso
    Se o item do meio for 50
        Retornar verdadeiro
    Sendo contrário, se 50 < item do meio
        Buscar metade esquerda
    Sendo contrário, se 50 > item do meio
        Buscar metade direita
  

  • Eventualmente, não teremos mais partes da matriz sobrando (se o item que queremos não estiver lá), para que possamos retornar falso.
  • Caso contrário, podemos pesquisar cada metade dependendo do valor do item do meio.

Big O

• Na semana 0, vimos diferentes tipos de algoritmos e seus tempos de execução:
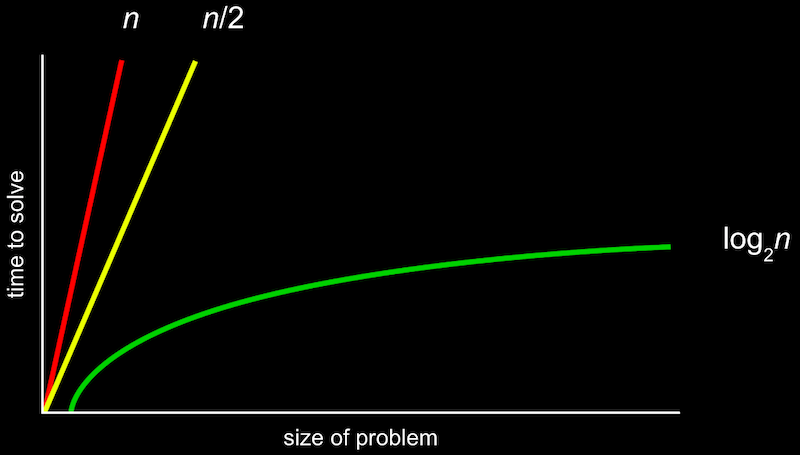
• A maneira mais formal de descrever isso é com a notação big O, que podemos entender como “da ordem de”. Por exemplo, se nosso algoritmo for a pesquisa linear, ele levará aproximadamente O(n) passos, "da ordem de n". Na verdade, até mesmo um algoritmo que examina dois itens por vez e leva n/2 passos tem O(n). Isso ocorre porque, à medida que n fica cada vez maior, somente o termo maior, n, importa.
• Da mesma forma, um tempo de execução logarítmico é O(log n), não importa qual seja a base, já que é apenas uma aproximação do que acontece quando n é muito grande.
• Existem alguns tempos de execução comuns: - O(_n_2) - O(n log n) - O(n) - (busca linear) - O(log n) - (busca binária) - O(1)
• Os cientistas da computação também podem usar a notação big Ω, big Omega, que é o limite inferior do número de etapas para nosso algoritmo. (Big O é o limite superior do número de etapas, ou o pior caso, e normalmente é o que mais nos importa.) Com a busca linear, por exemplo, o pior caso é n etapas, mas o melhor caso é 1 etapa, já que nosso item pode ser o primeiro item que verificamos. O melhor caso para a busca binária também é 1, já que nosso item pode estar no meio da matriz.
• E temos um conjunto semelhante dos tempos de execução big Ω mais comuns: - Ω(_n_2) - Ω(n log n) - Ω(n) - (contar o número de itens) - Ω(log n) - Ω(1) - (busca linear, busca binária)

Pesquisa linear

• Vamos dar uma olhada no numbers.c:

    #include <cs50.h>
    #include <stdio.h>
  
    int main(void)
    {
        // Uma matriz de números
        int numbers[] = {4, 8, 15, 16, 23, 42};
  
        // Pesquisar por 50
        for (int i = 0; i < 6; i++)
        {
            if (numbers[i] == 50)
            {
                printf("Encontrado\n");
                return 0;
            }
        }
        printf("Não encontrado\n");
        return 1;
    }
  

  • Aqui inicializamos uma matriz com alguns valores e verificamos os itens na matriz um de cada vez, em ordem.
  • E em cada caso, dependendo se o valor foi encontrado ou não, podemos retornar um código de saída de 0 (para sucesso) ou 1 (para falha).

• Podemos fazer o mesmo para nomes:

    #include <cs50.h>
    #include <stdio.h>
    #include <string.h>
  
    int main(void)
    {
        // Uma matriz de nomes
        string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"};
  
        // Pesquisar por EMMA
        for (int i = 0; i < 4; i++)
        {
            if (strcmp(names[i], "EMMA") == 0)
            {
                printf("Encontrado\n");
                return 0;
            }
        }
        printf("Não encontrado\n");
        return 1;
    }
  

  • Não podemos comparar strings diretamente, pois elas não são um tipo de dados simples, mas sim uma matriz de vários caracteres. Precisamos compará-las de forma diferente. Felizmente, a biblioteca string tem uma função strcmp que compara strings para nós e retorna 0 se forem iguais, então podemos usá-la.

• Vamos tentar implementar uma agenda telefônica com as mesmas ideias:

    #include <cs50.h>
    #include <stdio.h>
    #include <string.h>
  
    int main(void)
    {
        string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"};
        string numbers[] = {"617–555–0100", "617–555–0101", "617–555–0102", "617–555–0103"};
  
        for (int i = 0; i < 4; i++)
        {
            if (strcmp(names[i], "EMMA") == 0)
            {
                printf("Encontrado %s\n", numbers[i]);
                return 0;
            }
        }
        printf("Não encontrado\n");
        return 1;
    }
  

  • Usaremos strings para números de telefone, pois elas podem incluir formatação ou ser muito longas para um número.
  • Agora, se o nome em um determinado índice na matriz names corresponder a quem estamos procurando, retornaremos o número de telefone na matriz numbers, no mesmo índice. Mas isso significa que precisamos ter muito cuidado para garantir que cada número corresponda ao nome em cada índice, especialmente se adicionarmos ou removermos nomes e números.

Structs

• Acontece que podemos criar nossos próprios tipos de dados personalizados chamados structs:

    #include <cs50.h>
    #include <stdio.h>
    #include <string.h>
  
    typedef struct
    {
        string name;
        string number;
    }
    person;
  
    int main(void)
    {
        person people[4];
  
        people[0].name = "EMMA";
        people[0].number = "617–555–0100";
  
        people[1].name = "RODRIGO";
        people[1].number = "617–555–0101";
  
        people[2].name = "BRIAN";
        people[2].number = "617–555–0102";
  
        people[3].name = "DAVID";
        people[3].number = "617–555–0103";
  
        // Buscar por EMMA
        for (int i = 0; i < 4; i++)
        {
            if (strcmp(people[i].name, "EMMA") == 0)
            {
                printf("Encontrado %s\n", people[i].number);
                return 0;
            }
        }
        printf("Não encontrado\n");
        return 1;
    }
  

  • Podemos pensar em structs como contêineres que podem armazenar vários outros tipos de dados.
  • Aqui, criamos um novo tipo utilizando uma struct chamada person, que terá uma string chamada name e uma string chamada number. Em seguida, podemos criar uma array com esses tipos de struct e inicializar os valores presentes em cada uma delas utilizando uma nova sintaxe, ., para acessar as propriedades de cada person.
  • Em nosso loop, podemos agora ter mais certeza de que o number corresponde ao name, visto que pertencem ao mesmo elemento person.

Ordenação

• Se nossa entrada for uma lista não ordenada de números, há muitos algoritmos que poderíamos usar para produzir uma saída de uma lista ordenada.
• Com oito voluntários no palco com os seguintes números, poderíamos considerar a troca de pares de números próximos como o primeiro passo.

• Nossos voluntários começam na seguinte ordem aleatória:

    6 3 8 5 2 7 4 1
  

• Observamos os primeiros dois números e os trocamos para que fiquem em ordem:

    6 3 8 5 2 7 4 1
    – –
    3 6 8 5 2 7 4 1
  

• O próximo par, 6 e 8, está em ordem, por isso, não precisamos trocá-los.

• O próximo par, 8 e 5, precisa ser trocado:

    3 6 8 5 2 7 4 1
        – –
    3 6 5 8 2 7 4 1
  

• Continuamos até o final da lista:

    3 6 5 2 8 7 4 1
            – –
    3 6 5 2 7 8 4 1
              – –
    3 6 5 2 7 4 8 1
                – –
    3 6 5 2 7 4 1 8
  

• Nossa lista ainda não está ordenada, mas estamos um passo mais perto da solução porque o valor mais alto, 8, foi deslocado para a direita.

• Repetimos com outra passagem pela lista:

    3 6 5 2 7 4 1 8
    – –
    3 6 5 2 7 4 1 8
      – –
    3 5 6 2 7 4 1 8
        – –
    3 5 2 6 7 4 1 8
          – –
    3 5 2 6 7 4 1 8
            – –
    3 5 2 6 4 7 1 8
                – –
    3 5 2 6 4 1 7 8
  

  • Note que não precisamos trocar 3 e 6, ou 6 e 7.

• Agora, o próximo maior valor, 7, foi movido para a direita. Se repetirmos isso, cada vez mais da lista fica ordenada e, rapidamente, teremos uma lista totalmente ordenada.

• Esse algoritmo é chamado de bubble sort, em que os valores altos "borbulham" para a direita. O pseudocódigo para ele pode ser:

    Repetir n - 1 vezes
        Para i de 0 a n - 2
            Se os ésimos e ésimo + 1 elementos estiverem fora de ordem
                Trocá-los
  

  • Como estamos comparando os elementos ésimo e ésimo + 1, precisamos subir apenas até n - 2 para i. Em seguida, trocamos os dois elementos se estiverem fora de ordem.
  • E podemos parar depois que tivermos feito n - 1 passagens, já que sabemos que os maiores n - 1 elementos terão borbulhado para a direita.

• Temos n - 2 etapas para o laço interno e n - 1 laços, então temos um total de n2 - 3n + 2 etapas. Mas o maior fator, ou termo dominante, é n2, à medida que n fica cada vez maior, então, podemos dizer que o bubble sort é _O_(_n_2).

• Vimos tempos de execução como o seguinte, portanto, embora a pesquisa binária seja muito mais rápida que a pesquisa linear, pode não valer o custo único de ordenar a lista primeiro, a menos que façamos muitas pesquisas ao longo do tempo:
  • O(_n_2)
    • bubble sort
  • O(n log n)
  • O(n)
    • pesquisa linear
  • O(log n)
    • pesquisa binária
  • O(1)
• E o Ω para bubble sort ainda é n2, já que ainda verificamos cada par de elementos por n - 1 passagens.

Classificação por seleção

• Podemos adotar outra abordagem com o mesmo conjunto de números:

    6 3 8 5 2 7 4 1
  

• Primeiro, vamos analisar cada número e lembrar do menor número que vimos. Em seguida, podemos trocá-lo pelo primeiro número em nossa lista, já que sabemos que ele é o menor:

    6 3 8 5 2 7 4 1
    –             –
    1 3 8 5 2 7 4 6
  

• Agora sabemos que pelo menos o primeiro elemento de nossa lista está no lugar certo, então podemos procurar o menor elemento entre os demais e trocá-lo pelo próximo elemento não classificado (agora o segundo elemento):

    1 3 8 5 2 7 4 6
      –     –
    1 2 8 5 3 7 4 6
  

• Podemos repetir isso várias vezes até termos uma lista classificada.

• Esse algoritmo é chamado de classificação por seleção, e podemos escrever o pseudocódigo da seguinte forma:

    Para i de 0 até n–1
        Encontre o menor item entre o item i e o último item
        Troque o menor item pelo item i
  

• Com a grande notação O, ainda temos tempo de execução de O(n_2), já que estávamos olhando para aproximadamente todos os elementos _n para encontrar o menor e fazendo n passagens para classificar todos os elementos.

• Mais formalmente, podemos usar algumas fórmulas para mostrar que o maior fator é realmente _n_2:

    n + (n – 1) + (n – 2) + ... + 1
    n(n + 1)/2
    (n^2 + n)/2
    n^2/2 + n/2
    O(n^2)
  

• Portanto, descobrimos que a classificação por seleção é fundamentalmente igual à classificação por bolhas no tempo de execução:

  • O(_n_2)
    • Classificação por bolhas, classificação por seleção
  • O(n log n)
  • O(n)
    • Pesquisa linear
  • O(log n)
    • Pesquisa binária
  • O(1)
• O melhor caso, Ω, também é _n_2.

• Podemos voltar à classificação por bolhas e mudar seu algoritmo para algo assim, o que nos permitirá parar mais cedo se todos os elementos forem classificados:

    Repetir até que não haja trocas
        Para i de 0 a n–2
            Se os elementos i e i+1 estiverem fora de ordem
                Troque-os
  

• Agora, só precisamos analisar cada elemento uma vez, então o melhor caso agora é Ω(n): - Ω(_n_2) - Classificação por seleção - Ω(n log n) - Ω(n) - Classificação por bolhas - Ω(log n) - Ω(1) - Pesquisa linear, pesquisa binária

• Analisamos uma visualização on-line comparando algoritmos de classificação com animações de como os elementos se movem dentro dos arrays para a classificação por bolhas e a classificação por seleção.

Recursão

• Lembre-se que na semana 0, tínhamos um pseudocódigo para encontrar um nome em uma lista telefônica, onde tínhamos linhas nos dizendo para "voltar" e repetir alguns passos:

    1  Pegue a lista telefônica
    2  Abra a lista telefônica no meio
    3  Veja a página
    4  Se Smith estiver na página
    5      Ligue para Mike
    6  Senão se Smith estiver antes no livro
    7      Abra no meio da metade esquerda do livro
    8      **Volte para a linha 3**
    9  Senão se Smith estiver depois no livro
    10     Abra no meio da metade direita do livro
    11     **Volte para a linha 3**
    12 Senão
    13     Sair
  

• Em vez disso, poderíamos repetir todo o nosso algoritmo na metade do livro que nos restou:

    1  Pegue a lista telefônica
    2  Abra a lista telefônica no meio
    3  Veja a página
    4  Se Smith estiver na página
    5      Ligue para Mike
    6  Senão se Smith estiver antes no livro
    7      **Procure na metade esquerda do livro**
    8
    9  Senão se Smith estiver depois no livro
    10     **Procure na metade direita do livro**
    11
    12 Senão
    13     Sair
  

  • Isso parece um processo cíclico que nunca terminará, mas, na verdade, estamos dividindo o problema pela metade a cada vez e parando quando não houver mais livro.

• Recursão ocorre quando uma função ou algoritmo se refere a si mesmo, como no novo pseudocódigo acima.

• Também na semana 1, implementamos uma "pirâmide" de blocos na seguinte forma:

    #
    ##
    ###
    ####
  

  • E poderíamos ter um código iterativo como este:

      #include <cs50.h>
      #include <stdio.h>
    
      void draw(int h);
    
      int main(void)
      {
          // Obtenha a altura da pirâmide
          int height = get_int("Altura: ");
    
          // Desenhe a pirâmide
          draw(height);
      }
    
      void draw(int h)
      {
          // Desenhar pirâmide de altura h
          for (int i = 1; i <= h; i++)
          {
              for (int j = 1; j <= i; j++)
              {
                  printf("#");
              }
              printf("\n");
          }
      }
    

    • Aqui, usamos loops for para imprimir cada bloco em cada linha.

• Mas observe que uma pirâmide de altura 4 é na verdade uma pirâmide de altura 3, com uma linha extra de 4 blocos adicionados. E uma pirâmide de altura 3 é uma pirâmide de altura 2, com uma linha extra de 3 blocos. Uma pirâmide de altura 2 é uma pirâmide de altura 1, com uma linha extra de 2 blocos. E, finalmente, uma pirâmide de altura 1 é apenas uma pirâmide de altura 0, ou nada, com outra linha de um único bloco adicionado.

• Com essa ideia em mente, podemos escrever:

    #include <cs50.h>
    #include <stdio.h>
  
    void draw(int h);
  
    int main(void)
    {
        // Obtenha a altura da pirâmide
        int height = get_int("Altura: ");
  
        // Desenhe a pirâmide
        draw(height);
    }
  
    void draw(int h)
    {
        // Se não há nada para desenhar
        if (h == 0)
        {
            return;
        }
  
        // Desenhe uma pirâmide de altura h - 1
        draw(h - 1);
  
        // Desenhe mais uma linha de largura h
        for (int i = 0; i < h; i++)
        {
            printf("#");
        }
        printf("\n");
    }
  

  • Agora, nossa função draw primeiro se chama recursivamente, desenhando uma pirâmide de altura h - 1. Mas, antes disso, precisamos parar se h for 0, pois não haverá mais nada para ser desenhado.
  • Depois, desenhamos a próxima linha, ou uma linha de largura h.

Ordenação por mesclagem

• Podemos aplicar a ideia de recursão para ordenação, com outro algoritmo chamado ordenação por mesclagem. O pseudocódigo pode se parecer com:

    Se apenas um item
      Retornar
    Caso contrário
        Ordenar a metade esquerda dos itens
        Ordenar a metade direita dos itens
        Mesclar as metades ordenadas
  

• Veremos melhor isso na prática com uma lista não ordenada:

    7 4 5 2 6 3 8 1
  

• Primeiro, ordenaremos a metade esquerda (os primeiros quatro elementos):

    7 4 5 2 | 6 3 8 1
    – – – –
  

• Bem, para ordenar, precisamos ordenar primeiro a metade dos elementos da metade esquerda:

    7 4 | 5 2 | 6 3 8 1
    – –
  

• Agora, temos apenas um item, 7, na metade esquerda, e um item, 4, na metade direita. Portanto, vamos mesclar isso, pegando primeiro o menor item de cada lista:

    – – | 5 2 | 6 3 8 1
    4 7
  

• E agora voltamos para a metade direita da metade esquerda, e a ordenamos:

    – – | – – | 6 3 8 1
    4 7 | 2 5
  

• Agora, ambas as metades da metade esquerda estão ordenadas, então podemos mesclá-las. Observamos o início de cada lista e pegamos 2, pois é menor que 4. Então, pegamos 4, já que agora é o menor item na frente de ambas as listas. Em seguida, pegamos 5 e, finalmente, 7, para obter:

    – – – – | 6 3 8 1
    – – – –
    2 4 5 7
  

• Agora ordenamos a metade direita da mesma forma. Primeiro, a metade esquerda da metade direita:

    – – – – | – – | 8 1
    – – – – | 3 6 |
    2 4 5 7
  

• Então, a metade direita da metade direita:

    – – – – | – – | – –
    – – – – | 3 6 | 1 8
    2 4 5 7
  

• Podemos mesclar a metade direita agora:

    – – – – | – – – –
    – – – – | – – – –
    2 4 5 7 | 1 3 6 8
  

E finalmente, podemos unir as duas metades da lista inteira, seguindo as mesmas etapas de antes. Note que não precisamos verificar todos os elementos de cada metade para encontrar o menor, pois sabemos que cada metade já está classificada. Em vez disso, pegamos apenas o menor elemento dos dois no início de cada metade:

    – – – – | – – – –
    – – – – | – – – –
    2 4 5 7 | – 3 6 8
    1


    – – – – | – – – –
    – – – – | – – – –
    – 4 5 7 | – 3 6 8
    1 2


    – – – – | – – – –
    – – – – | – – – –
    – 4 5 7 | – – 6 8
    1 2 3


    – – – – | – – – –
    – – – – | – – – –
    – – 5 7 | – – 6 8
    1 2 3 4


    – – – – | – – – –
    – – – – | – – – –
    – – – 7 | – – 6 8
    1 2 3 4   5


    – – – – | – – – –
    – – – – | – – – –
    – – – 7 | – – – 8
    1 2 3 4   5 6


    – – – – | – – – –
    – – – – | – – – –
    – – – – | – – – 8
    1 2 3 4   5 6 7


    – – – – | – – – –
    – – – – | – – – –
    – – – – | – – – –
    1 2 3 4   5 6 7 8

Demorou muitas etapas, mas na verdade demorou menos etapas do que os outros algoritmos que vimos até agora. Dividimos nossa lista pela metade a cada vez, até que estávamos "classificando" oito listas com um elemento cada:

    7 | 4 | 5 | 2 | 6 | 3 | 8 | 1
    4   7 | 2   5 | 3   6 | 1   8
    2   4   5   7 | 1   3   6   8
    1   2   3   4   5   6   7   8

Como nosso algoritmo dividiu o problema pela metade a cada vez, seu tempo de execução é logarítmico com O(log n). E depois que classificamos cada metade (ou metade de uma metade), precisávamos mesclar todos os elementos, com n etapas, pois tínhamos que olhar para cada elemento uma vez. Portanto, nosso tempo total de execução é O(n log n): - O(_n_2) - classificação por bolha, classificação por seleção - O(n log n) - classificação por mesclagem - O(n) - busca linear - O(log n) - busca binária - O(1) Como log n é maior que 1, mas menor que n, n log n está entre n (vezes 1) e _n_2. O melhor caso, Ω, ainda é n log n, pois ainda classificamos cada metade primeiro e depois as mesclamos: - Ω(_n_2) - classificação por seleção - Ω(n log n) - classificação por mesclagem - Ω(n) - classificação por bolha - Ω(log n) - Ω(1) - busca linear, busca binária Finalmente, há outra notação, Θ, Theta, que usamos para descrever os tempos de execução dos algoritmos se o limite superior e o limite inferior forem os mesmos. Por exemplo, a classificação por mesclagem tem Θ(n log n) já que o melhor e o pior caso requerem o mesmo número de etapas. E a classificação por seleção tem Θ(_n_2). Analisamos uma visualização final de algoritmos de classificação com um número maior de entradas, rodando ao mesmo tempo.