Aula 5

• Ponteiros
• Redimensionar matrizes
• Estruturas de dados
• Listas vinculadas
• Mais estruturas de dados

Ponteiros

• Da última vez, aprendemos sobre ponteiros, malloc e outras ferramentas úteis para trabalhar com memória.

• Vamos rever este trecho de código:

    int main(void)
    {
        int *x;
        int *y;
  
        x = malloc(sizeof(int));
  
        *x = 42;
        *y = 13;
    }
  

  • Aqui, as primeiras duas linhas de código em nossa função main estão declarando dois ponteiros, x e y. Então, alocamos memória suficiente para um int com malloc e armazenamos o endereço retornado por malloc em x.
  • Com *x = 42;, vamos ao endereço apontado por x e armazenamos o valor 42 nesse local.

  • A linha final, porém, é bugada, pois não sabemos qual é o valor de y, já que nunca definimos um valor para ele. Em vez disso, podemos escrever:

      y = x;
      *y = 13;
    

    • E isso irá definir y para apontar para o mesmo local que x faz, e então definir esse valor como 13.

• Damos uma olhada em um clipe curto, Diversão com Ponteiros com Binky, que também explica este trecho de uma forma animada!

Redimensionando arrays

• Na semana 2, aprendemos sobre arrays, onde poderíamos armazenar o mesmo tipo de valor em uma lista lado a lado. Mas precisamos declarar o tamanho dos arrays quando os criamos e, quando quisermos aumentar o tamanho do array, a memória ao redor dele poderá ser ocupada por outros dados.
• Uma solução pode ser alocar mais memória em uma área maior que esteja livre e mover nosso array para lá, onde há mais espaço. Mas precisamos copiar nosso array, o que se torna uma operação com tempo de execução O(n), uma vez que precisamos copiar cada um dos n elementos em um array.

• Podemos escrever um programa como o seguinte para fazer isso em código:

    #include <stdio.h>
    #include <stdlib.h>
  
    int main(void)
    {
        // Aqui, alocamos memória suficiente para três inteiros, e nossa variável
        // list apontará para o primeiro inteiro.
        int *list = malloc(3 * sizeof(int));
        // Devemos verificar se alocamos a memória corretamente, pois o malloc pode
        // falhar ao obter memória livre suficiente.
        if (list == NULL)
        {
            return 1;
        }
  
        // Com esta sintaxe, o compilador fará aritmética de ponteiro para nós e
        // calculará o byte na memória que list[0], list[1] e list[2] mapeia,
        // já que os inteiros têm 4 bytes de tamanho.
        list[0] = 1;
        list[1] = 2;
        list[2] = 3;
  
        // Agora, se quisermos redimensionar nosso array para 4 inteiros, tentaremos alocar
        // memória suficiente para eles e usar temporariamente tmp para apontar para o primeiro:
        int *tmp = malloc(4 * sizeof(int));
        if (tmp == NULL)
        {
            return 1;
        }
  
        // Agora, copiamos inteiros do array antigo para o novo array ...
        for (int i = 0; i < 3; i++)
        {
            tmp[i] = list[i];
        }
  
        // ... e adicionamos o quarto inteiro:
        tmp[3] = 4;
  
        // Devemos liberar a memória original para list, por isso precisamos de
        // uma variável temporária para apontar para o novo array ...
        free(list);
  
        // ... e agora podemos definir nossa variável list para apontar para o novo array que
        // tmp aponta:
        list = tmp;
  
        // Agora, podemos imprimir o novo array:
        for (int i = 0; i < 4; i++)
        {
            printf("%i\n", list[i]);
        }
  
        // E finalmente, liberar a memória para o novo array.
        free(list);
    }
  

• Acontece que na verdade há uma função útil, realloc, que realocará alguma memória:

    #include <stdio.h>
    #include <stdlib.h>
  
    int main(void)
    {
        int *list = malloc(3 * sizeof(int));
        if (list == NULL)
        {
            return 1;
        }
  
        list[0] = 1;
        list[1] = 2;
        list[2] = 3;
  
        // Aqui, fornecemos ao realloc nosso array original que list aponta, e ele
        // retornará um novo endereço para um novo array, com os dados antigos copiados:
        int *tmp = realloc(list, 4 * sizeof(int));
        if (tmp == NULL)
        {
            return 1;
        }
        // Agora, tudo o que precisamos fazer é lembrar o local do novo array:
        list = tmp;
  
        list[3] = 4;
  
        for (int i = 0; i < 4; i++)
        {
            printf("%i\n", list[i]);
        }
  
        free(list);
    }
  

Estruturas de dados

• Estruturas de dados são construções de programação que nos permitem armazenar informações em diferentes layouts na memória do nosso computador.
• Para construir uma estrutura de dados, precisaremos de algumas ferramentas que já vimos:
  • struct para criar tipos de dados personalizados
  • . para acessar propriedades em uma estrutura
  • * para ir para um endereço na memória apontado por um ponteiro

Listas Vinculadas

• Com uma lista vinculada, podemos armazenar uma lista de valores que pode ser facilmente aumentada armazenando valores em partes diferentes da memória:
  
  • Isso é diferente de uma matriz, pois nossos valores não estão mais próximos uns dos outros na memória.
• Podemos vincular nossa lista alocando, para cada elemento, memória suficiente para o valor que desejamos armazenar e o endereço do próximo elemento:
  
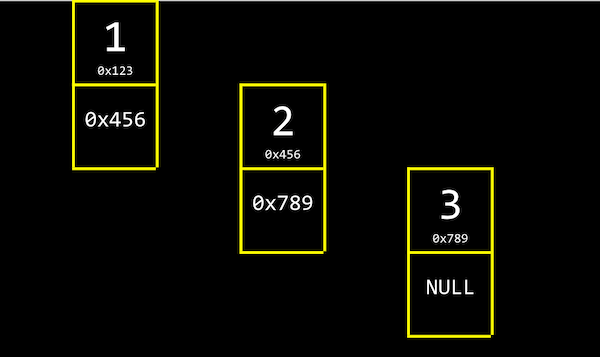
  • A propósito, NUL se refere a \0, um caractere que encerra uma string, e NULL se refere a um endereço todo zero ou um ponteiro nulo que podemos considerar como não apontando para lugar nenhum.
• Ao contrário dos arrays, não acessamos mais elementos aleatoriamente em uma lista vinculada. Por exemplo, não podemos mais acessar o quinto elemento da lista calculando onde ele está, em tempo constante. (Como sabemos que os arrays armazenam elementos consecutivos, podemos adicionar 1 ou 4 ou o tamanho do nosso elemento para calcular endereços.) Em vez disso, temos que seguir o ponteiro de cada elemento, um de cada vez. E precisamos alocar o dobro de memória do que precisávamos antes para cada elemento.

• No código, podemos criar nossa própria struct chamada node (como um nó de um gráfico em matemática) e precisamos armazenar um int e um ponteiro para o próximo node chamado next:

    typedef struct node
    {
        int number;
        struct node *next;
    }
    node;
  

  • Iniciamos esta struct com typedef struct node para que possamos nos referir a um node dentro de nossa struct.

• Podemos construir uma lista vinculada no código começando com nossa struct. Primeiro, queremos lembrar uma lista vazia para que possamos usar o ponteiro nulo: node *list = NULL;.

• Para adicionar um elemento, primeiro precisamos alocar um pouco de memória para um nó e definir seus valores:

    node *n = malloc(sizeof(node));
    // Queremos ter certeza de que o malloc conseguiu obter memória para nós:
    if (n != NULL)
    {
        // Isso é equivalente a (*n).number, onde primeiro vamos ao nó apontado
        // por n e então definimos a propriedade number. Em C, também podemos usar essa
        // notação de seta:
        n->number = 2;
        // Então precisamos armazenar um ponteiro para o próximo nó em nossa lista, mas o
        // novo nó não apontará para nada (por enquanto):
        n->next = NULL;
    }
  

• Agora nossa lista pode apontar para este nó: list = n;:
  

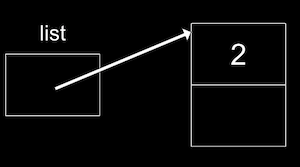
• Para adicionar à lista, criaremos um novo nó da mesma forma, talvez com o valor 4. Mas agora precisamos atualizar o ponteiro em nosso primeiro nó para apontar para ele.

• Como nosso ponteiro list aponta apenas para o primeiro nó (e não podemos ter certeza de que a lista tem apenas um nó), precisamos "seguir as migalhas de pão" e seguir o ponteiro next de cada nó:

    // Cria um ponteiro temporário para onde list está apontando
    node *tmp = list;
    // Enquanto o nó tiver um ponteiro next ...
    while (tmp->next != NULL)
    {
        // ... defina o temporário para o próximo nó
        tmp = tmp->next;
    }
    // Agora, tmp aponta para o último nó em nossa lista, e podemos atualizar seu próximo
    // ponteiro para apontar para nosso novo nó.
  

• Se quisermos inserir um nó na frente de nossa lista vinculada, precisaremos atualizar cuidadosamente nosso nó para apontar para aquele que o segue, antes de atualizar a lista. Caso contrário, perderemos o resto da nossa lista:

    // Aqui, estamos inserindo um nó na frente da lista, então queremos seu
    // próximo ponteiro para apontar para a lista original, antes de apontar a lista para
    // n:
    n->next = list;
    list = n;
  

• E para inserir um nó no meio de nossa lista, podemos percorrer a lista, seguindo cada elemento um de cada vez, comparando seus valores e alterando os ponteiros next cuidadosamente também.

• Com alguns voluntários no palco, simulamos uma lista, com cada voluntário atuando como a variável list ou um nó. À medida que inserimos nós na lista, precisamos de um ponteiro temporário para seguir a lista e garantir que não perdamos nenhuma parte dela. Nossa lista vinculada aponta apenas para o primeiro nó em nossa lista, então só podemos olhar para um nó por vez, mas podemos alocar dinamicamente mais memória conforme precisamos para aumentar nossa lista.

• Agora, mesmo que nossa lista ligada seja ordenada, o tempo de execução de sua pesquisa será O(n), pois temos que seguir cada nó para verificar seus valores e não sabemos onde será o meio da nossa lista.

• Podemos combinar todos os nossos trechos de código em um programa completo:

    #include<stdio.h>
    #include<stdlib.h>
  
    // Representa um nó
    typedef struct node
    {
        int number;
        struct node *next;
    }
    node;
  
    int main(void)
    {
        // Lista de tamanho 0, inicialmente não aponta para nada
        node *list = NULL;
  
        // Adicionar número à lista
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = 1;
        n->next = NULL;
        // Criamos nosso primeiro nó, armazenamos o valor 1 nele e deixamos o próximo
        // ponteiro para apontar para nada. Então, nossa variável de lista pode apontar para ele.
        list = n;
  
        // Adicionar número à lista
        n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = 2;
        n->next = NULL;
        // Agora, vamos ao nosso primeiro nó para o qual list aponta e definimos o próximo ponteiro
        // nele para apontar para nosso novo nó, adicionando-o ao final da lista:
        list->next = n;
  
        // Adicionar número à lista
        n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = 3;
        n->next = NULL;
        // Podemos seguir vários nós com esta sintaxe, usando o next ponteiro
        // repetidamente, para adicionar nosso terceiro novo nó ao final da lista:
        list->next->next = n;
        // Normalmente, porém, queremos um loop e uma variável temporária para adicionar
        // um novo nó à nossa lista.
  
        // Imprimir lista
        // Aqui podemos iterar sobre todos os nós em nossa lista com um temporário
        // variável. Primeiro, temos um ponteiro temporário, tmp, que aponta para o
        // lista. Então, nossa condição para continuar é que tmp não seja NULL, e
        // finalmente, atualizamos tmp para o próximo ponteiro dele mesmo.
        for (node *tmp = list; tmp != NULL; tmp = tmp->next)
        {
            // Dentro do nó, vamos apenas imprimir o número armazenado:
            printf("%i\n", tmp->number);
        }
  
        // Lista livre
        // Como estamos liberando cada nó à medida que avançamos, usaremos um loop while
        // e siga o próximo ponteiro de cada nó antes de liberá-lo, mas veremos
        // isso com mais detalhes no Problema definido 5.
        while (list != NULL)
        {
            node *tmp = list->next;
            free(list);
            list = tmp;
        }
    }
  

Mais estruturas de dados

• Uma árvore é outra estrutura de dados em que cada nó aponta para dois outros nós, um à esquerda (com um valor menor) e outro à direita (com um valor maior):
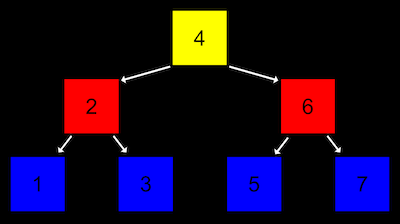
  • Observe que agora há duas dimensões nesta estrutura de dados, em que alguns nós estão em "níveis" diferentes de outros. E podemos imaginar a implementação disso com uma versão mais complexa de um nó em uma lista vinculada, em que cada nó não tem um, mas dois ponteiros, um para o valor no "meio da metade esquerda" e outro para o valor no "meio da metade direita". E todos os elementos à esquerda de um nó são menores, e todos os elementos à direita são maiores.
  • Isso é chamado de árvore de pesquisa binária porque cada nó tem no máximo dois filhos, ou nós para os quais está apontando, e uma árvore de pesquisa porque é classificada de uma forma que nos permite pesquisar corretamente.
  • E como uma lista vinculada, queremos manter um ponteiro apenas para o início da lista, mas neste caso queremos apontar para a raiz, ou nó do topo central da árvore (o 4).

• Agora, podemos facilmente fazer uma pesquisa binária e, como cada nó está apontando para outro, também podemos inserir nós na árvore sem precisar mover todos eles, como teríamos que fazer em um array. Pesquisar recursivamente nesta árvore se parece com algo como:

    typedef struct node
    {
        int number;
        struct node *left;
        struct node *right;
    } node;
  
    // Aqui, *tree é um ponteiro para a raiz da nossa árvore.
    bool search(node *tree)
    {
        // Precisamos de um caso base, se a árvore atual (ou parte da árvore) for NULL,
        // para retornar falso:
        if (tree == NULL)
        {
            return false;
        }
        // Agora, dependendo se o número no nó atual é maior ou menor,
        // podemos apenas olhar para o lado esquerdo ou direito da árvore:
        else if (50 < tree->number)
        {
            return search(tree->left);
        }
        else if (50 > tree->number)
        {
            return search(tree->right);
        }
        // Caso contrário, o número deve ser igual ao que estamos procurando:
        else {
            return true;
        }
    }
  

• O tempo de execução de busca em árvore é O(log n), e inserir nós e manter a árvore balanceada também é O(log n). Gastando um pouco mais de memória e tempo para manter a árvore, nós obtemos agora uma busca mais rápida do que em uma lista ligada simples.

• Uma estrutura de dados com tempo de execução de busca quase constante é uma tabela de hash, que é uma combinação de uma matriz e uma lista ligada. Nós temos uma matriz de listas ligadas, e cada lista ligada na matriz possui elementos de uma certa categoria. Por exemplo, no mundo real, nós podemos ter muitas etiquetas de nomes e podemos classificá-las em 26 blocos, cada um rotulado com uma letra do alfabeto, então podemos encontrar etiquetas de nomes verificando apenas um bloco.
• Nós podemos implementar isto em uma tabela de hash com uma matriz de 26 ponteiros, cada um dos quais aponta para uma lista ligada para uma letra do alfabeto:
  
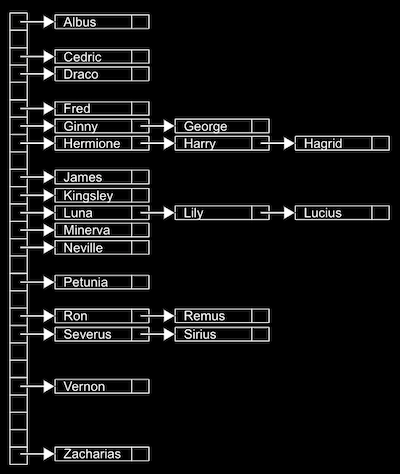
• Como nós temos acesso aleatório com matrizes, podemos adicionar elementos rapidamente, e também indexar rapidamente em um bloco.
• Um bloco pode ter múltiplos valores correspondentes, então nós vamos usar uma lista ligada para armazenar todos eles horizontalmente. (Nós chamamos isso de colisão, quando dois valores correspondem de alguma forma.)
• Isto é chamado de tabela de hash porque nós usamos uma função de hash, que pega uma entrada e a mapeia para um bloco em que ela deve ir. No nosso exemplo, a função de hash está apenas verificando a primeira letra do nome, então ela pode retornar 0 para “Albus” e 25 para “Zacharias”.
• Mas no pior caso, todos os nomes podem começar com a mesma letra, então nós podemos acabar com o equivalente de uma única lista ligada novamente. Nós podemos verificar as primeiras duas letras, e alocar blocos suficientes para 26*26 possíveis valores de hash, ou até mesmo as primeiras três letras, e agora vamos precisar de 26*26*26 blocos. Mas nós ainda podemos ter um pior caso onde todos os nossos valores começam com os mesmos três caracteres, então o tempo de execução para busca é O(n). Na prática, entretanto, nós podemos chegar mais perto de O(1) se nós tivermos tantos blocos quanto valores possíveis, especialmente se nós tivermos uma função de hash ideal, onde nós podemos classificar nossas entradas em blocos únicos.
• Nós podemos usar outra estrutura de dados chamada de trie (pronunciada como “try”, abreviação de “recuperação”):
  
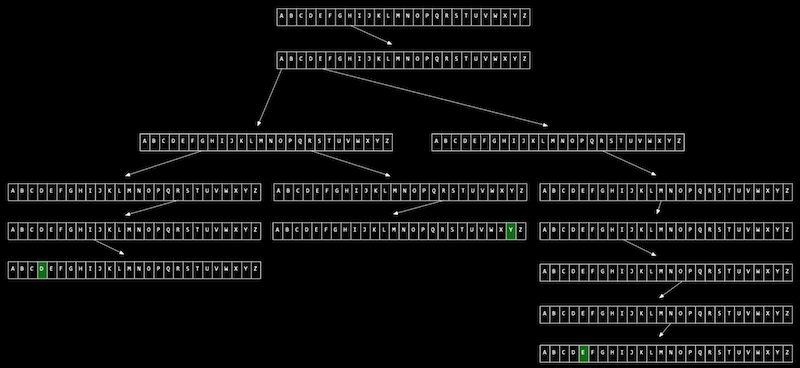
  • Imagine que nós queremos armazenar um dicionário de palavras eficientemente, e ser capaz de acessar cada uma em tempo constante. Uma trie é como uma árvore, mas cada nó é uma matriz. Cada matriz terá cada letra, A-Z, armazenada. Para cada palavra, a primeira letra apontará para uma matriz, onde a próxima letra válida apontará para outra matriz, e assim por diante, até que cheguemos a algo indicando o final de uma palavra válida. Se a nossa palavra não estiver na trie, então uma das matrizes não terá um ponteiro ou um caractere de término para a nossa palavra. Agora, mesmo que nossa estrutura de dados tenha muitas palavras, o tempo de busca será apenas o comprimento da palavra que estamos procurando, e este pode ser um máximo fixo, então nós temos O(1) para busca e inserção. O custo para isso, no entanto, é 26 vezes mais memória do que precisamos para cada caractere.
• Há construções de nível ainda mais alto, estruturas de dados abstratas, onde nós usamos nossos blocos de construção de matrizes, listas ligadas, tabelas de hash e tries para implementar uma solução para algum problema.
• Por exemplo, uma estrutura de dados abstrata é uma fila, onde nós queremos adicionar e remover valores de forma “primeiro a entrar, primeiro a sair” (FIFO). Para adicionar um valor, nós podemos enfileirá-lo, e para remover um valor, nós vamos desenfileirá-lo. E nós podemos implementar isso com uma matriz que redimensionamos conforme adicionamos itens, ou uma lista ligada onde nós acrescentamos valores ao final.
• Uma estrutura de dados “oposta” seria uma pilha, onde itens adicionados mais recentemente (empurrados) são removidos (retirados) primeiro, de forma “último a entrar, primeiro a sair” (LIFO). Nossa caixa de entrada de e-mail é uma pilha, onde nossos e-mails mais recentes estão no topo.
• Outro exemplo é um dicionário, onde nós podemos mapear chaves a valores, ou strings a valores, e podemos implementar um com uma tabela de hash onde uma palavra vem com algumas outras informações (como sua definição ou significado).
• Nós vamos assistir a “Jack aprende os fatos sobre filas e pilhas”, uma animação sobre essas estruturas de dados.